Solutions 2: Exploring Compartmental Model Dynamics

Sam Abbott

Source: vignettes/solutions-two.Rmd

Learning Objectives

  1. Understand how changing parameter values, and model structure, can influence model dynamics.
  2. Understand the dynamics of the SEIR model in detail.
  3. Understand the impact of risk group stratification on model dynamics.
  4. Understand some of the complex dynamics produced by a more realistic model.

Outline for Session

  1. Set up (5 minutes)
  2. Investigate the dynamics of a simple SEIR model (20 minutes)
  3. Explore the impact of adding high and low risk latency to a SEIR model, in comparison to the SEIR model (10 minutes).
  4. Investigate the complex dynamics of a more realistic SHLIR model (10 minutes) .
  5. Explore the parameter space of multiple models and try to understand some of the general implications of model structures on dynamics (10 minutes).
  6. Session wrap up (5 minutes)

Solutions

The practical solutions are in bold, all code has been completed and the exercise models have been simmulated and summarised.

Set up

In order to more systematically explore the parameter space of multiple models we have provided an interactive interface. Start the interactive interface by running the following in R.

if (!library(shiny, logical.return = TRUE)) {
  install.packages("shiny")
  library(shiny)
}
shiny::runGitHub("exploreidmodels", "seabbs")

If having problems running the application then talk to an instructor and/or try the hosted web version (http://seabbs.co.uk/shiny/exploreidmodels/).

Use this interface to answer the following excercises. Instructions for using the interactive interface can be found in the about section of the application.

Exercises

1. A Simple SEIR Model of Tuberculosis (TB)

As a first exercise, we are going to explore the simple SEIR model (select it in the interface), as seen in the design a model practical. For reference the SEIR model flow diagram seen in the first practical’s solutions has been provided.[1] The code for this model can be found in the code section of the interactive interface.

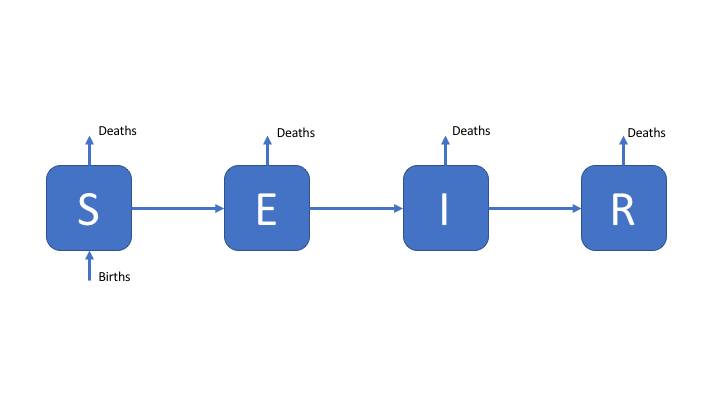
Figure 1: An SEIR model of TB transmission, including simple demographic processes

Figure 1: An SEIR model of TB transmission, including simple demographic processes

Explore

Model dynamics are parameter dependent. Even in a simplistic model like the one outlined above parameter values can greatly alter the dynamics. Answer the following questions by varying the parameters and rerunning the model (Note: Don’t worry if you can’t use the interface to the exact values given below) .

  1. Set a transmission rate (beta) of 7, an infectious period of 3 months, and a latent period of 0. What role does the exposed (latent) compartment have with these settings? What happens to the number of susceptibles over time?

    • It plays no role. In effect this is an SIR model.
    • The number of susceptibles decreases over time. Initially this happens at a slow rate, which then increases dramatically before slowing.

  2. Increase the transmission rate and rerun the model. How does this impact the number of infected individuals?

    • Increasing the transmission rate increases the total number of cases, increases the maximum size of the epidemic peak, and speeds up the outbreak.

  3. Increase the infectious period. How does a longer infectious period impact the shape of the epidemic curve?

    • Increasing the infectious period increases the size of the epidemic peak and extends the duration of the epidemic. There is little impact on the initial spread of the disease outbreak.

  4. Increase the latent period to 6 months. What impacts does this have on the disease outbreak?

    • The cumulative number of the cases is comparable but the epidemic duration is longer, with a lower epidemic peak. The initial outbreak is also slower.

  5. Set beta to 3, the infectious period to 12 months, the latent period to 0, and set the timespan to 100. Run the model, turn on demographic processes, and then re-run the model. What is the impact of adding demographic processes (births and deaths)?

    • Introducing demographic processes leads to oscillations in all compartments. In particular this leads to mulitple secondary disease outbreaks after the primary outbreak.

  6. Reduce the life expectancy to 20 years. What impact does this have on the infected population?

    • The initial epidemic is unchanged. However, the secondary outbreaks occur more frequently and there is a higher average number of cases at any given time.

2. Add High and Low Risk Compartments

To make the SEIR model slightly more realistic, and therefore better able to capture the observed dynamics of TB, we add a second latent population (as discussed in the solutions for practical 1). This change can be seen in the model flow diagram (Figure 2). Go back to practical 1 if you need a refresher for the motivation behind this. We have also added reinfection for the low risk latent population.

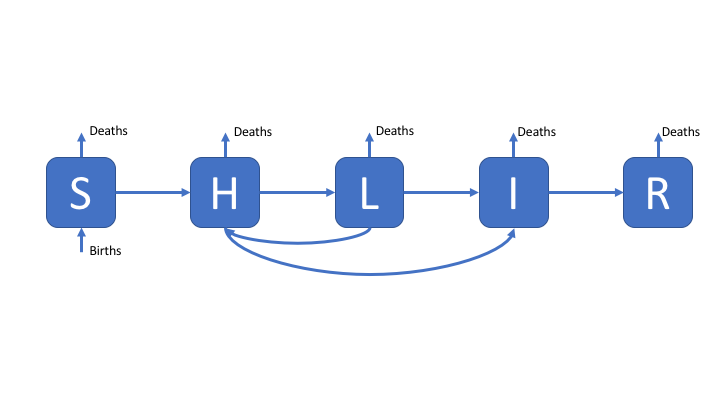
Figure 2: An SHLIR model of TB transmission, including simple demographic processes

Figure 2: An SHLIR model of TB transmission, including simple demographic processes

Explore

  1. Switch to the SHLIR model and turn off demographic processes. Set beta to 9, the high risk latent period to 0, the low risk latent period to 20 years, the infectious period to 12 months, and the timespan to 100 years. Run this model (this is effectively the SEIR model, see the flow diagram to understand why). Now set the high risk latent period to 2 years, and the rate of developing active disease when high risk to 0.6 - re-run the model. What is the impact of the second high risk latent compartment?

    • Without the high risk latent compartment the outbreak is very slow, with a flat curve shape. Adding the high risk latent compartment speeds up the epidemic and increases the outbreak size.

  2. Re-run the model with demographic processes (with a life expectancy of 20 years). What impact do they have on the dynamics?

    • As for the SEIR model demographic processes lead to oscillations in all population compartments and an increase in the average number of cases after the intial outbreak. Demographic processes in this model prevent cases from becoming permanently protected by their latent disease.

3. A more realistic SHLIR model flow diagram

The most complex model supported by the interactive interface, this is a more realistic model that might be used in research. The SHLIR model flow diagram (Figure 3) includes: risk groups, treatment, and reinfection for those who have recovered from active disease. Whilst many realistic TB models use age structure this is not included here (if you are interested in discussing how you would include this talk to your instructors or contact me). For simplicity we have assumed that it is possible to be born into both populations. For the motivation behind this model see practical 1.

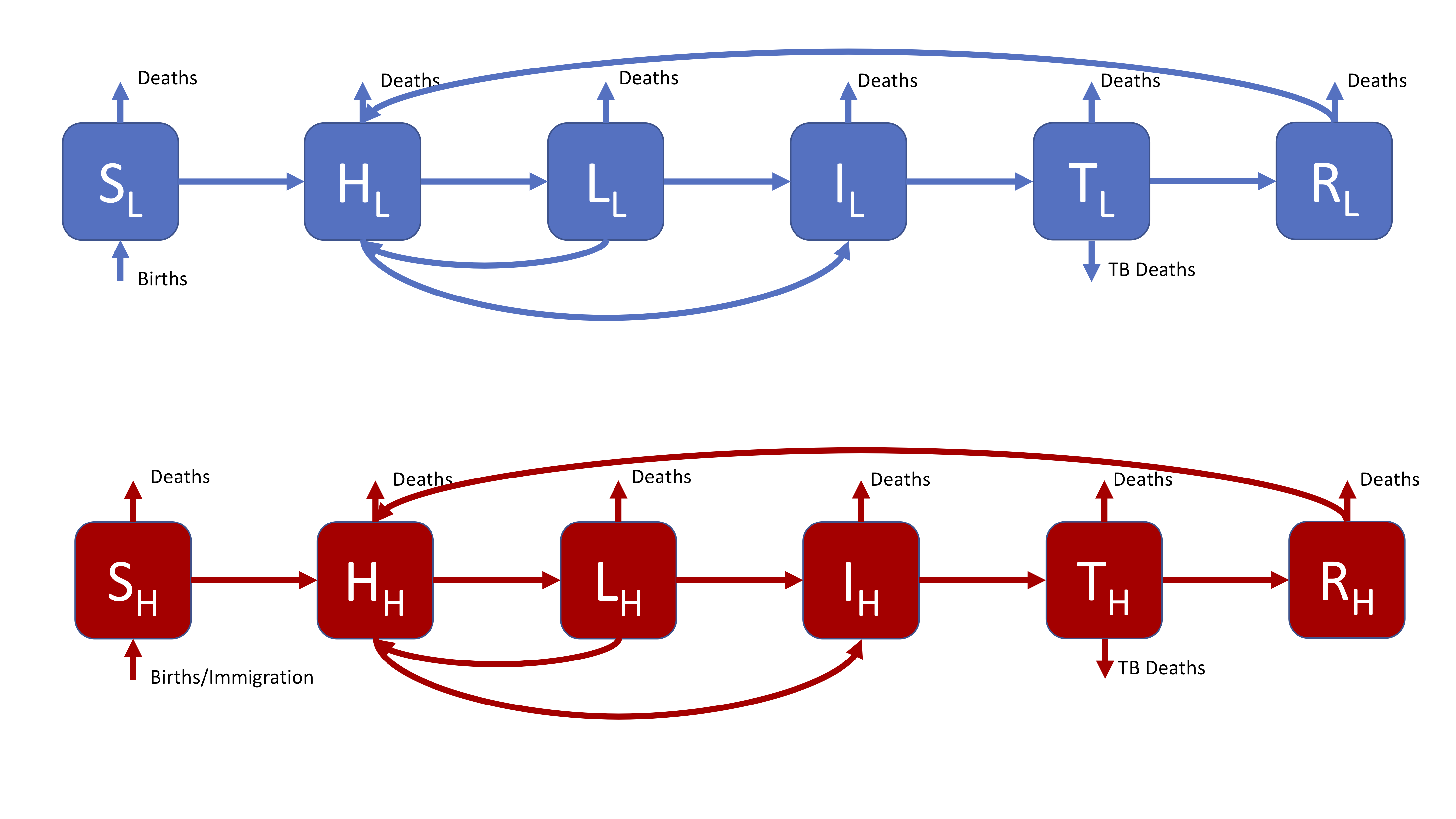
Figure 3: A realistic SHLIR model of TB transmission, including simple demographic processes

Figure 3: A realistic SHLIR model of TB transmission, including simple demographic processes

Figure 3 does not include the interaction between the high and low risk subgroups as this is through the force of infection. The force of infection is defined as,

\[ \lambda_i = \beta \sum_{j = L, H}M_{ij}I_j \]

Where \(\lambda_i\) is the force of infection in each risk group (\(i = L, H\)) and \(M_{LH}\) is the mixing rate between risk groups. It is assumed that within group contact rates are equivalent and defined such that,

\[ M_{ii} = 1 \]

It is also assumed that the between group contact rates are defined as (where \(i \neq j\)),

\[ M_{ij} = 0.1 \]

Explore

  1. Select the SHLITR model with risk groups. Run it with a beta of 3, a high risk beta of 3, a life expectancy of 1000, and all other parameters as set. Re-run the model with a high risk beta of 30. What is the impact of the high risk group on the number of cases?

    • Increasing the transmission rate in the high risk group increased the number of cases in both the low risk and high risk populations.

  2. Set beta to be 0.5, the between group mixing to be 0 and run the model. Now set the between group mixing to be 0.2 and re-run the model. With these parameter settings what differences do you see between these model runs? Can you explain these findings (see the model outline above for hints)?

    • For both models runs there is a large outbreak in the high risk group. In the low risk group there is no outbreak without mixing but a large outbreak when between group mixing is accounted for.
    • The large outbreak in the low risk population, observed when risk groups mix, is driven by the introduction of high risk cases to the force of infection. In this situation, even if the disease completely dies out in the low risk population, transmission can still occur.

  3. What is the impact of increasing or decreasing the between group mixing parameter in the above scenario?

    • As mixing is reduced the proportion of the low risk population that are infected is reduced.
    • As mixing is increased the disease dynamics become more homogeneous between groups.

4. Explore model dynamics

The interactive interface allows for exploration of multiple other models, using it can you identify some commonalities between different models? What generalisations can you draw from these commonalities?

  • Adding birth and death process can lead to oscillating behaviour around some steady state.
  • Adding additional latent compartments reduces the speed of progression of the epidemic through the population.
  • Highly infectious disease may die out in a short space of time if there is not a sufficient number of susceptibles.
  • Identified any others? Talk through them with your instructors.

References

1 Brooks-Pollock E, Cohen T, Murray M. The impact of realistic age structure in simple models of tuberculosis transmission. PLoS One 2010;5:3–8. doi:10.1371/journal.pone.0008479